(1)
This article discusses our proposed generic method for generating a Mamdani-Type fuzzy rules-base by applying the Symbiotic Evolution method, interested readers are referred to my papers on Symbiotic Evolution [3-5]. More information can be sent out on your request (MasoudEmail).
Symbiotic Evolution (SE) is inspired by nature. In an ecological unit, species work together towards some common aims. However, in order to survive and produce their offsprings, they have to adapt themselves to the changing environment. In this process, there are symbiotic relations between individuals such as competition, exploitation, and benefiting. The relations are commonly called symbiosis [1].
In order to apply SE within a rule-base generation context, each chromosome in the population should represent only one fuzzy rule and not the whole fuzzy rule-base. As Moriarty [2] showed, partial solutions can be characterized as specializations. This method maintains the diversity of the population, as no single fuzzy rule can perform well alone. Thus, SE prevents the population from converging to sub-optimal solutions. In addition, Genetic Algorithm can search many different areas concurrently. The form of a fuzzy set with Gaussian membership functions is illustrated in equation (1) ,
|
(1) |
where xi is the input fuzzy variable, y is the output fuzzy variable,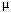 
(.) is a Gaussian membership function with the center ci and the standard deviation (or the width) si. The parameters of each membership function are encoded into a chromosome as shown in Figure 1 , ci and si are the parameters of the input fuzzy variables and co and so are the parameters of the output fuzzy variable. Therefore, each individual in the population represents only a partial solution to the problem.
 |
However, in the conventional methods each chromosome consists of a complete set of fuzzy rules as shown in Figure 1 b. In the SE algorithm, the population sets up a pool of promising rules that are randomly initialized for the first generation.
Randomly selecting and combining Nr chromosomes from the population constructs an Nr-rule Fuzzy Inference System (FIS). The performance of the generated FIS is then evaluated, and based on its performance, an equal fitness score is assigned to all contributing rules. This latter evaluates each FIS until NFIS randomly set up fuzzy rule-bases are all evaluated. The overall fitness of an individual is calculated by averaging its fitnesses over all the FISs where it has contributed. At this point, the GA is ready to select the fittest rules and reproduce the next generation of rules; we included the tournament selection method for mating the fittest individuals. The usual crossover and mutation operations are also applied. However, with the aim of obtaining a better performance within a minimum number of generations, the Selective Breeding method is used; in this algorithm, individuals from the old generation and the offsprings are combined and the best individuals are selected to represent the new generation.
References:
[1] Hirasawa, K., Y. Ishikawa, J. Hu, J. Murata, and J. Mao, “Genetic symbiosis algorithm,” The 2000 Congress on Evolutionary Computation, La Jolla, CA, USA, pp. 1377-1384, 2000.
[2] Moriarty, D. E. and R. Miikkulainen, “Efficient reinforcement learning through symbiotic evolution,” Machine learning, vol. 22, pp. 11-32, 1996.
[3] "Elicitation and Fine-Tuning of Mamdani-Type Fuzzy Rules Using Symbiotic Evolution", European Symposium on Intelligent Technologies, Hybrid Systems and their implementation on Smart Adaptive Systems (EUNITE 2001), 13 - 14 December 2001, Tenerife, Spain.
[4] "Rule-Base Generation via Symbiotic Evolution for a Mamdani-Type Fuzzy Control System",
Proceedings of the 10th IEEE International Conference on Fuzzy Systems (FUZZ-IEEE01), 2-5th December 2001, Melbourne, Australia.
[5] " Elicitation and fine-tuning of fuzzy control rules using symbiotic evolution", Fuzzy Sets and Systems, 147 (2004) pp. 57-74.